Die zwei Berge

Der Ursprung vieler mathematischer Werkszeuge, die uns selbstverständlich geworden sind, ist nicht selten in Vergessenheit geraten, wenn er nicht mittlerweile mit dem Anstrich des Mystischen, Unsinnigen und Nutzlosen versehen worden ist. So auch geschehen mit den Polygonalzahlen, einer Erfindung der Pythagoräer, die heute noch als Quadrat- und Kubikzahlen im Gebrauch sind.

Dem an Kabbala oder Numerologie Interessierten werden die sogenannten "Mystischen Zahlen" ein Begriff sein, bei denen es sich schlicht um Trigonalzahlen handelt. Von den Pythagoräern stammt auch die Definition, dass die Summe aller Zahlen 1 bis n immer eine Trigonalzahl ist. Ebenfalls die Regel: Die Summe aller ungeraden Zahlen 1 bis n ergibt eine Quadratzahl, wobei sich aus solchen Summen sämtliche n Quadrate bilden lassen. Das ist fast nicht verwunderlich, denn beide basieren letztlich auf derselben räumlichen Struktur, nur jeweils in andren Richtungen, was offensichtlich wird, wenn man erst mal Tetraeder und Pyramiden gebildet hat.

Deshalb werde ich auch nicht von Pentagonalzahlen reden, die im Grunde doch einer anderen Klasse angehören. Die Rede wird von Hexagonalzahlen sein und auch nicht der einfachen Folge derselben, sondern einer abwechselnden Folge mit - von mir so genannten - Pseudohexagonen, sowie einer sich dazu parallel verhaltenden Folge von Quasihexagonen, welche sich mit Pseudoquasihexagonen abwechseln. Das Trigon 6 ist in dieser Anordnung ein Pseudoquasihexagon, das Trigon 3 ein Pseudohexagon und die 1 - wie sich zeigt - ein Hexagon und die 0 ein Pseudohexagon. Hexagone und Quasihexagone sind zwölffach symmetrisch, Pseudo-Formen dagegen nur sechsfach symmetrisch. Die Menge der Pseudo-Formen ist eine größere infinite Menge als die Normalformen. Trotzdem kommen sie nur in gleicher Anzahl wie die Normalformen zur Anwendung. Man könnte sagen: "Sie dienen als Mörtel". Treffender ist wohl: "Sie sind verdreht".

Quasihexagone sind weitestgehend mit den Hexagonen identisch, mit dem Unterschied, dass ihnen sechs Elemente an den Ecken fehlen. Warum sollten diese Figuren eine Relevanz haben? Nun, weil es neben der Folge der Hexagone die einzige derartige Folge mit gleichen Symmetrien und der nächsten Annäherung an den Kreis (d.h. um ein Zentrum gruppiert) ist (ansonsten ließen sich selbstverständlich beliebige Anordnungen verschiedenartigster Symmetrie anfertigen). Diese Begründung hinkt zugegebenermaßen ein wenig. Die eigentliche Begründung bzw. der Ausgangspunkt der Untersuchung wird weiter unten im Text beschrieben. Bis dahin gehen wir ruhig einmal davon aus, dass die beiden sich ähnlich zueinander verhalten wie Tetraeder und Pyramide, von deren gemeinsamen Struktur es genau nur diese beiden regelmäßigen Ausformungen gibt. Die Struktur der beiden Berge (so nenne ich sie mal) ist nahezu gleich, nur das sich die Ausrichtung pro Schicht einmal dreht, was wiederum die Pseudoformen erzeugt.

Zunächst also die beiden Folgen oder "Berge". Die Summen wurden zu Skalen zusammengefasst: Hier Hauptskala L (Hexagone) und Hauptskala A (Quasihexagone) genannt (warum L & A, wird weiter unten geklärt). Die Differenz zwischen beiden Skalen auf jeder Schicht 6. Die Gnomone (in hellblau) sind bei beiden Skalen identisch. Man kann sie auf eine jeweils abwechselnde Iteration (in Orange) um 1 bzw. 2 zurückverfolgen:

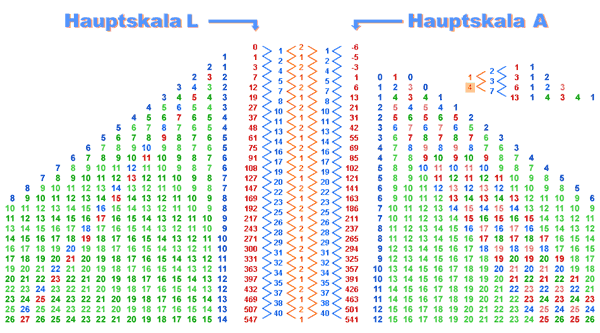
Nun ist auffallend an dieser Darstellung, dass Hauptskala A scheinbar im negativen Bereich beginnt und nicht einfach mit 0 aufhört wie Hauptskala L. Hier haben wir ein primitives Beispiel dafür, wie negative Zahlen anfangen einen "metaphysischen" Bereich zu beschreiben. Zunächst sei auf die zweite Abbildung verwiesen, die unter anderem zeigt, das beide Skalen nicht bei 0 und -6 enden, sondern das 0 und -6 Scheitelpunkte zweier unendlicher Skalen sind. 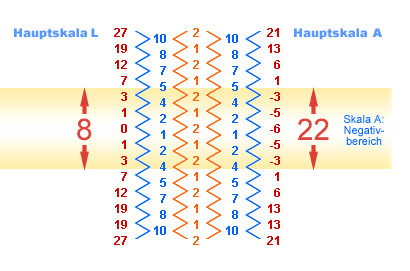Man könnte sich die beiden Berge quasi als Gebilde von aufeinanderzuwachsenden unendlich langen Stalagmiten und Stalaktiten vorstellen, bei denen Hexagone fast vor der Berührung stehen, die Quasihexagone jedoch noch ein Stück weit auseinander sind, getrennt von einem quantitätsseitig nennbaren Etwas aus zuwenig "Materie", welche jedoch von Seite der Form "undefinierbar" bleibt. Es lassen sich keine Hexagone aus 5 bilden (wenn man mal eine "Negativ-Welt" unterstellen wollte). -5 ist schlicht 1 - 6, ebenso wie -3 = 3 - 6 ist etc.. Auch ließ sich aus den vorhergehenden Schichten der Algorithmus nicht weiter ausführen, so der eine nachvollziehbar fiktive Negativ-Anordnung ergeben hätte. Eigentlich ließ er sich gar nicht weiter ausführen (Fehlermeldung). Währe die -5 nicht, ich währe ja glatt noch drauf reingefallen...

Aber reingefallen bin ich ohnehin. Denn ich muss zugeben, dass ich anfangs auch die Hauptskala A mit 1 beginnen lassen habe. Ich wollte ursprünglich alle gültigen Skalen ermitteln, welche von 1 ausgehen und meines Erachtens als zweite Schicht auf 1 folgend nur eine 3 haben konnten. Dabei sind ursprünglich die beiden Hauptskalen entstanden. Andere ergaben sich nicht. Diese Anordnung findet in den vier Schichten 1, 3, 6, 13 rechts als kleine Extradarstellung in selber Höhe.

Erst mit dem Nachvollziehen der Gnomone ist mir die Unterbrechung in der Regelmäßigkeit der Iteration aufgefallen (siehe die gelb markierte 4 bei den Iteratoren), der meine heiß geliebte 3 als falsch denunzierte. Das brachte mich erst dahin die Iteration bis in den Negativbereich zu verfolgen, den Scheitelpunkt zu entdecken usw..

Den Negativbereich fand ich ja durchaus aufregend. Da führte nun ein Experiment an konkret in der Realität auftretenden Quantitäten zu unrealen, gewissermaßen "metaphysischen" Ergebnissen. Für jemanden, der versucht der Kabbala auf die Schliche zu kommen, scheint sich dabei zumindest ein Teilerfolg anzukündigen. Aber das Wegfallen von der 3 empfand ich doch als so unschön, so dass ich bereits im Begriffe war, an diesen Sachverhalt etwas hineinzuinterpretieren. Dann ging mir auf, das mir ein Fehler unterlaufen war, weil mir eine Bedingung für beide Gebilde noch nicht klar war: In der Mitte dürfen zwei Schichten keinen Oktaeder erzeugen. Ich bin also der tetraederischen Struktur auf den Leim gegangen. Also bestand kein Zweifel mehr: Auf die 6 musste die 1 folgen. So hat mich denn wohl die 3 zu einer Skala geführt, in der die 3 selber in Wahrheit gar nicht vorkommt. Oder hatte Skala A überhaupt eine Gültigkeit?

Nun sollte ich nicht versäumen zu erwähnen, dass ich seinerzeit noch nicht geknackt hatte und verzweifelt auf der Suche nach einer 22 mit berechtigtem Bedeutungsanspruch war. 21 und 23 taten sich zuhauf auf. Jedoch die 22 weigerte sich, in irgendeinem nicht künstlich herbeigeführten Kontext aufzutauchen. Beim Addieren des Negativbereichs von Skala A tauchte sie dann endlich auf: -3 - 5 -6 -5 - 3 = -22 (siehe die zweite Abbildung oben). Die Kabbala kennt eigentlich weder Negativzahlen, noch kennt sie tatsächlich die 0. Jedoch über die Tarot Trümpfe ließen sich hervorragende Analogien aufbauen: 0 XXII 22. Wo währen negative Ideen in einem rein positiven System besser aufgehoben, als bei der 0? Die 0 als Abyssos zum "Jenseitigen", "Metaphysischen", zur "Gegenwelt", zur Antimaterie: Dahinter steckten Gedankenspiele, dass sich die 0 von AIN in DAATH wiederspiegeln könnte. Würde man eine planetare Zuordnung zu XXII wagen, würde möglicherweise passen: Siehe Crowleys Anordnung von auf DAATH.

Bei Skala L auf der anderen Seite ergab sich der Wert 8. Wenn, wie oben beschrieben, 0 XXII gilt, dann muss hier VIII gelten und VIII . Somit währe nun auch die Benennung der Skalen geklärt. Beinahe zwangsläufig drängt sich auch das Wort auf.

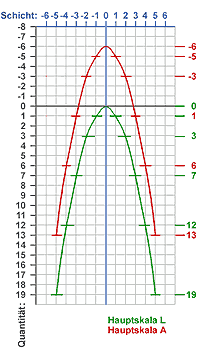
Nun, das war Anlass genug, die beiden Skalen in eine andere Darstellung zu übertragen. Das ganze Gebilde quasi um 90° gedreht, jede Schicht als eine Position auf der X-Achse aufgefasst und die entsprechenden Quantitäten der beiden Hauptskalen auf der Y-Achse eingetragen, ergab sich die Darstellung mit zwei Parabeln (welche keine Normalparabeln sind) in Abbildung C. Hätte meine ursprüngliche Version von Skala A Gültigkeit behalten, würde sie sich die entsprechende Parabel knapp über der grünen von Skala L einfügen. Als ich das Diagramm schließlich angefertigt hatte, kamen mir die Parabeln irgendwie bekannt vor: Ich ein paar Monate vorher in den Trümpfen I und X ein Kartenpaar ausgemacht, welches sich als solches offenbart, wenn man die beiden Karten an den Fußenden zusammenlegt. Nur eine Parabel hatte ich darin nicht gesehen und schon recht nicht ein Parabel-Paar.

Das war natürlich ebenfalls ein Ergebnis der Jagt nach der 22. Der Zusammenhang hier erschließt sich über eine Identifikation von Dionysos sowohl mit Hermes wie auch mit Zeus. Zu der Assoziationskette Dionysos Zeus 0 siehe Crowleys Kommentar zu Trumpf 0 im Buch Thoth und meinen Text über . In aller Kürze: In vielerlei Hinsicht repräsentiert Dionysos IO DIO DEUS (Gott) ZEUS die Archaischen Frühformen des ursprünglichen Wettergottes Zeus/Jupiter (woraus sich auch die Zuordnung auf das Element erschließt). Merkur ist zwar weniger ein Wettergott, dafür eindeutig ein Schöpfergott (als Schöpfer der Wirklichkeit. "Wirklichkeit" "Illusion"). Aus der Mythologie sind Hermes und Zeus bekannt für ihre Streiche. Beide haben ein hohes Interesse für das profane Leben in niederen Regionen, bis hinunter zu den Menschen: Als Botschafter einerseits, als Verführer oder Betrüger andererseits. Im Hexagramm der Planeten liegen sich und genau gegenüber. Die zugeordneten Buchstaben 20 und 2 ergeben 2 + 20 = 22. Ganz nebenbei: X + I = XI (siehe Liber Al 1.60, 2.16) und 22 : 2 = 11 (natürlich).

Ich hatte bereits festgestellt, dass der Abyssos sich bei Kartenpaaren zwischen den bildlichen Darstellungen befinden kann, also quasi im Passepartout. Nun war die Frage spannend: Wenn meine beiden Parabeln sich tatsächlich in dem Kartenpaar wiederfinden würden, müsste sich auch mein Abyssos in den Parabeln, also der Bereich <= 0, in das Passepartout einfügen. Das Ergebnis war verblüffend. Nicht allein das sich mein Parabelpaar, an deren Gültigkeit ich zwischenzeitlich sehr gezweifelt hatte, sich im Kartenpaar wiederfand. Es fand sich in den Proportionen sogar zweimal wieder (entsprechend dem großen und dem kleinen Lebensbaum auf denen die Entwürfe aufgebaut sind). Und scheinbar hatte auch Crowley seine Parabeldarstellungen bei 13 bzw. 19 aufhören lassen.